På denna sida finns det en länk där man kan anmäla sig för omtenta. Det måste alltså alla som vill göra tentan i Växjö göra.
Innan 13 april!
Och som man kan se nu är dit i sal D2236/D2266 (vårt hus alltså, på andra våningen).
Updatering: omtentan och lösningsförslag ligger nu på kurssidan. Jag sätter betyg i helgen.
torsdag 8 april 2010
tisdag 6 april 2010
Omtenta lördag 24 april; kursutvärdering
Omtenta blir en salstenta på lördag 24 april. De som vill göra tentan på sin skola eller lärcenter kan göra den i vecka 17.
För kursutvärdering vill jag gärna ha feedback från alla, båda campus och distans. Ni kan mejla mig, skicka post, lämna lappar eller lämna kommentarer nedan.
Själv tycker jag att det har varit bättre än mina tidigare distanskurser, där jag ofta kände att jag inte gjorde tillräckligt för distansstudenterna - ge dem en bok i handen, och de gör en tenta, och får poäng för sådant som de redan visste. Jag hade och har inkörningsstrul med tekniken, men på grunderna har fungerat. Och jag tror att det också har varit bra för campusstudenter.
Vad jag inte är särskilt nöjd med är dock resultaten på första tentan: det var nio som klarade den. Två VG (båda distansstudenter), och sju G (fyra distans, tre campus), av 23 som gjorde tentan. Visst, några frågor var svårare, men jag har inte funnit anledning att avvika från min standardgräns på minst 50 % rätt.
Så, kom gärna med feedback om hur det kan bli bättre nästa gång.
För kursutvärdering vill jag gärna ha feedback från alla, båda campus och distans. Ni kan mejla mig, skicka post, lämna lappar eller lämna kommentarer nedan.
Själv tycker jag att det har varit bättre än mina tidigare distanskurser, där jag ofta kände att jag inte gjorde tillräckligt för distansstudenterna - ge dem en bok i handen, och de gör en tenta, och får poäng för sådant som de redan visste. Jag hade och har inkörningsstrul med tekniken, men på grunderna har fungerat. Och jag tror att det också har varit bra för campusstudenter.
Vad jag inte är särskilt nöjd med är dock resultaten på första tentan: det var nio som klarade den. Två VG (båda distansstudenter), och sju G (fyra distans, tre campus), av 23 som gjorde tentan. Visst, några frågor var svårare, men jag har inte funnit anledning att avvika från min standardgräns på minst 50 % rätt.
Så, kom gärna med feedback om hur det kan bli bättre nästa gång.
måndag 29 mars 2010
Lösningar på tentan
Lösningsförslag för tentamensfrågorna ligger på på kurssidan (pdf-länkar längst ner). Jag har nu fått in alla, och sätter betygen idag.
tisdag 16 mars 2010
Stråloptikuppgifter i Bengtsson
Lämpliga uppgifter i Bengtsson kap 35 och 36 har efterfrågats.
"Questions" är kvalitativa. Några är lite svårare än i Hewitt, men fråga bara här om det är problem med vissa.
Av de nämnde delkapitlar, bör ni kunna uppgifter som är markerade med (I). Sedan finns det några (II) som är intressanta, till exempel 35.10. Och 35.15. Och i kapitel 36 är problem 13 om f-talen väl bra för allmänbildningen. I allmänhet är det att göra dessa uppgifter, och att diskutera om det behövs.
"Questions" är kvalitativa. Några är lite svårare än i Hewitt, men fråga bara här om det är problem med vissa.
Av de nämnde delkapitlar, bör ni kunna uppgifter som är markerade med (I). Sedan finns det några (II) som är intressanta, till exempel 35.10. Och 35.15. Och i kapitel 36 är problem 13 om f-talen väl bra för allmänbildningen. I allmänhet är det att göra dessa uppgifter, och att diskutera om det behövs.
onsdag 10 mars 2010
"Övningstentor"
Det efterfrågas förstås övningstentor. Problemet är att jag inte har gamla tentor liggande för den här kursen, med den här kurslitteraturen.
I höst hade jag dock en kurs på magisterprogrammet i elektroteknik. Fast det är uppenbart mer avancerat, var det också grundläggande, eftsersom dessa ingenjörer inte förväntas ha så mycket bakgrund inom optik. Å andra sidan var det en öppen-bok tenta, så jag räknade med att man kunde slå upp lite saker. Och resultaterna var ganska nedslående. Gamla tentan ligger på kurssidan. Kursen var på engelska.
Så det är för det allra mesta saker som ni inte behöver kunna, men typ hälften av lösningarna borde ni kunna hänga med i. Jag ger länken så att ni ska se hur mina tentaproblem brukar se ut. Jag ska också lägga till omtentan med lösningar.
I höst hade jag dock en kurs på magisterprogrammet i elektroteknik. Fast det är uppenbart mer avancerat, var det också grundläggande, eftsersom dessa ingenjörer inte förväntas ha så mycket bakgrund inom optik. Å andra sidan var det en öppen-bok tenta, så jag räknade med att man kunde slå upp lite saker. Och resultaterna var ganska nedslående. Gamla tentan ligger på kurssidan. Kursen var på engelska.
Så det är för det allra mesta saker som ni inte behöver kunna, men typ hälften av lösningarna borde ni kunna hänga med i. Jag ger länken så att ni ska se hur mina tentaproblem brukar se ut. Jag ska också lägga till omtentan med lösningar.
måndag 8 mars 2010
Vita material är transparenta material
Hewitts figur 28.10 är standard för att illustrera diffus reflektion, men det stämmer egentligen bara för matta metallytor och några andra totalt ogenomskinliga material. De vanliga fallen som snö, papper, salt, sand osv är lite mer komplicerade. I dessa faller handlar det om finfördelade transparenta ämnen.
Snö är ju egentligen bara vatten. Men det är finfördelat, med många ytor. Vid varje yta bryts ljuset, och det är bara en mindre del som direkt reflekteras. Sedan kommer nästa yta, och nästa, och ljusets bryts ett otalt antal gångar. Ljuset sprids diffusivt utan att det absorberas (bara lite i det röda, därför är ljuset blått nere i snön). Det är en slumpvandring, och det är lika mycket som sprids uppåt som nedåt. Det som sprids uppåt är diffus reflektion genom flerfaldig spridning (multiple scattering).
På samma sätt består papper av fibrer av genomskinlig cellulosa (jämför cellofan). Ljusets sprids av variationerna i brytningsindex. En droppe vatten (eller ännu bättre: matolja) minskar skillnaden i brytningsindex vid fibrernas ytor. Refraktionen blir mycket mindre, och ljuset går mer rakt igenom. Därför ser en oljefläck på papper mörk ut om det ligger på bordet, men ljusare när man håller pappret mot ljuset.
Även socker och salt är klart transparenta i form av större kristaller. Och sand är egentligen finfördelat kvarts, bergkristall.
Snö är ju egentligen bara vatten. Men det är finfördelat, med många ytor. Vid varje yta bryts ljuset, och det är bara en mindre del som direkt reflekteras. Sedan kommer nästa yta, och nästa, och ljusets bryts ett otalt antal gångar. Ljuset sprids diffusivt utan att det absorberas (bara lite i det röda, därför är ljuset blått nere i snön). Det är en slumpvandring, och det är lika mycket som sprids uppåt som nedåt. Det som sprids uppåt är diffus reflektion genom flerfaldig spridning (multiple scattering).
På samma sätt består papper av fibrer av genomskinlig cellulosa (jämför cellofan). Ljusets sprids av variationerna i brytningsindex. En droppe vatten (eller ännu bättre: matolja) minskar skillnaden i brytningsindex vid fibrernas ytor. Refraktionen blir mycket mindre, och ljuset går mer rakt igenom. Därför ser en oljefläck på papper mörk ut om det ligger på bordet, men ljusare när man håller pappret mot ljuset.
Även socker och salt är klart transparenta i form av större kristaller. Och sand är egentligen finfördelat kvarts, bergkristall.
lördag 6 mars 2010
Transparens och dispersion
Hewitt skriver i kapitel 26 ett avsnitt om transparenta material. Jag har inga större invändingar, men jag kan inte låta bli att ge en något mindre förenklad redogörelse.
Om man betraktar luft, är det 99,9 % vakuum (som vi sett i delen om ljud).

En mottagare känner en superposition av det elektriska fältet av den inkommande elektromagnetiska vågen och av fälten från svängningarna av laddningarna i alla luftmolekyler.
Luftmolekylerna har resonanser vid frekvenser i det ultravioletta området. Där sker absorption av strålning. Vid de lägre frekvenserna i det synliga området är molekylernas inducerade polarisering liten, och 90 grader ur fas med fältet. Elektronmolnens inducerade svängningar ger upphov till ett svagt fält som ligger 90 grader efter i fas. Summan av dessa två fält ligger lite efter i fas. Det gör att vågens hastighet (fashastigheten) är lite lägre i luft än i vakuum. Brytningsindex är större än 1 (1.0003 i luft vid STP).
Ju närmare resonansen frekvensen ligger, ju större är svängningarna. Därför är brytningsindex vanligtvis större för blått ljus än för rött ljus. Det kallas normal dispersion.

Om man betraktar luft, är det 99,9 % vakuum (som vi sett i delen om ljud).

En mottagare känner en superposition av det elektriska fältet av den inkommande elektromagnetiska vågen och av fälten från svängningarna av laddningarna i alla luftmolekyler.
Luftmolekylerna har resonanser vid frekvenser i det ultravioletta området. Där sker absorption av strålning. Vid de lägre frekvenserna i det synliga området är molekylernas inducerade polarisering liten, och 90 grader ur fas med fältet. Elektronmolnens inducerade svängningar ger upphov till ett svagt fält som ligger 90 grader efter i fas. Summan av dessa två fält ligger lite efter i fas. Det gör att vågens hastighet (fashastigheten) är lite lägre i luft än i vakuum. Brytningsindex är större än 1 (1.0003 i luft vid STP).
Ju närmare resonansen frekvensen ligger, ju större är svängningarna. Därför är brytningsindex vanligtvis större för blått ljus än för rött ljus. Det kallas normal dispersion.

torsdag 4 mars 2010
Ljusets brytning
Tyvärr var det så ofantligt stora mängder datastrul strax innan föreläsningen att jag glömde att sätta igång recording första timmen. Och det för en lektion som inte var så dålig. Jag ska skriva en sammanfattning här.

Bilden ovan visar refraktion. Sugröret ser knäckt eller avbrutet ut på två ställen. Men optikdiagram brukar visa ljusstrålarnas brytning. Det är mer abstrakt än vad man ser. Det är inte helt enkelt att gå fram och tillbaka mellan strålgångsdiagram och en vanlig bild på speglar eller glaskroppar. Men det det behövs för verklighetsförankring av ämnet. Gör därför ett försök med denna något kluriga uppgiften. (Lösning på måndag.)
Brytning uppstår för att ljus färdas långsammare i vatten eller i glas än i vakuum. Om brytningsindex är n (inget heltal här), har ljuset en hastighet i mediet som är c/n. Vågfronterna som man ritar i Huyghens konstruktion växer då långsammare.

Figuren ovan visar en strålknippe som faller snett in på en yta av ett transparant ämne. När strålknippens högra sida når ytan, har punkterna vid ytan på strålans vänstersida redan gjort stora ringar. Tangenten ger den nya vågfronten i materialet. Man kan så härleda Snells lag, att sinus av infallsvinkeln är n gånger sinus av den brutna strålens vinkel med normalen. (Gör detta!)
Vad som sker blir tydligare i en animering av vågfronter:

Våghastigheten på högersida är lägre än på vänstersidan. Frekvensen är lika överallt (kolla det!), så våglängden är mindre på högersida. Vågens utbredningsrikting ligger närmare normalen - strålen har brutits till normalen i det långsammare mediet, i enighet med Snells lag.

Bilden ovan visar refraktion. Sugröret ser knäckt eller avbrutet ut på två ställen. Men optikdiagram brukar visa ljusstrålarnas brytning. Det är mer abstrakt än vad man ser. Det är inte helt enkelt att gå fram och tillbaka mellan strålgångsdiagram och en vanlig bild på speglar eller glaskroppar. Men det det behövs för verklighetsförankring av ämnet. Gör därför ett försök med denna något kluriga uppgiften. (Lösning på måndag.)
Brytning uppstår för att ljus färdas långsammare i vatten eller i glas än i vakuum. Om brytningsindex är n (inget heltal här), har ljuset en hastighet i mediet som är c/n. Vågfronterna som man ritar i Huyghens konstruktion växer då långsammare.

Figuren ovan visar en strålknippe som faller snett in på en yta av ett transparant ämne. När strålknippens högra sida når ytan, har punkterna vid ytan på strålans vänstersida redan gjort stora ringar. Tangenten ger den nya vågfronten i materialet. Man kan så härleda Snells lag, att sinus av infallsvinkeln är n gånger sinus av den brutna strålens vinkel med normalen. (Gör detta!)
Vad som sker blir tydligare i en animering av vågfronter:

Våghastigheten på högersida är lägre än på vänstersidan. Frekvensen är lika överallt (kolla det!), så våglängden är mindre på högersida. Vågens utbredningsrikting ligger närmare normalen - strålen har brutits till normalen i det långsammare mediet, i enighet med Snells lag.
onsdag 3 mars 2010
Spegel, spegel
Pga av mjukvaruändringar kunde jag inte få kameran igång i måndags. Upptagningen har bara min röst och det som jag ritade på Smartboard. Här en sammanfattning.
Först spegellagen. Den reflekterade strålen ligger i samma plan som den infallande strålan och spegelytans normal. Reflektionsvinkeln är lika med infallsvinkeln. Det kan man se på olika sätt:
1) Tidssymmetri, inom optik strålgångens omvändbarhet;
2) Fermats princip (snabbaste väg, kortaste tid);
3) Huyghens princip (eller mer sofistikerade varianter av vågoptik)

Principen med snabbaste väg kan man utveckla via geometri (som ovan enligt Heron av Alexandria, och som i Hewitt) eller med hjälp av analys. Summan av AX + XB är minimal när dess derivata med hänseende på x är lika med noll. Uppgift: visa att detta leder till reflektionslagen.
Här en skiss på reflektion enligt Huyghens princip:

En stråle (blå pil) med plan vågfront kommer in från vänster. Punkter på spegelns yta börjar stråla, och ger upphov till en ny vågfront som lämnar till höger med samma vinkel som infallsvinkeln.
De reflekterade strålarna från en plan spegel verkar komma från en gemensam punkt bakom spegeln:

Det är en virtuell bild. Man kan inte projicera det på en skärm.
Det är annorlunda med en parallell stråle som faller in på en hålspegel:

Endast när infallsvinklarna är små går de reflekterade strålarna genom ett reellt fokus. Avvikelserna for större vinklar kallas sfärisk aberration. Någon aberration finns inte för parabeliska ytor när strålarna är parallela med den optiska axeln.
Hur man konstruerar en bild av ett föremål (konvex spegel):

Först spegellagen. Den reflekterade strålen ligger i samma plan som den infallande strålan och spegelytans normal. Reflektionsvinkeln är lika med infallsvinkeln. Det kan man se på olika sätt:
1) Tidssymmetri, inom optik strålgångens omvändbarhet;
2) Fermats princip (snabbaste väg, kortaste tid);
3) Huyghens princip (eller mer sofistikerade varianter av vågoptik)

Principen med snabbaste väg kan man utveckla via geometri (som ovan enligt Heron av Alexandria, och som i Hewitt) eller med hjälp av analys. Summan av AX + XB är minimal när dess derivata med hänseende på x är lika med noll. Uppgift: visa att detta leder till reflektionslagen.
Här en skiss på reflektion enligt Huyghens princip:

En stråle (blå pil) med plan vågfront kommer in från vänster. Punkter på spegelns yta börjar stråla, och ger upphov till en ny vågfront som lämnar till höger med samma vinkel som infallsvinkeln.
De reflekterade strålarna från en plan spegel verkar komma från en gemensam punkt bakom spegeln:

Det är en virtuell bild. Man kan inte projicera det på en skärm.
Det är annorlunda med en parallell stråle som faller in på en hålspegel:

Endast när infallsvinklarna är små går de reflekterade strålarna genom ett reellt fokus. Avvikelserna for större vinklar kallas sfärisk aberration. Någon aberration finns inte för parabeliska ytor när strålarna är parallela med den optiska axeln.
Hur man konstruerar en bild av ett föremål (konvex spegel):

fredag 26 februari 2010
"Elasticity"
Jag fick en fråga i mejl av Lina, som nog är av intresse för andra av er. Hon skriver:
Det är mycket möjligt att det finns en del skolböcker som säger att ljudhastigheten är högre i vatten pga densitet, men det är strunt. Jag har försökt förmedla till er att svängningshastigheter är högre ju starkare den återställande kraften är, och lägre ju större trögheten (massan) är. Det gäller för svängningar av massor på fjädrar, det gäller även för våghastigheter på strängar och i material. Våghastighet är omvänt proportionell mot roten ur densitet.
Det är den återställande kraften som är så mycket större i vatten än i luft. I en stav (is, stål) är det elasticitetsmodulen, som definieras som förhållandet mellan mekanisk spänning och töjning. Töjning är relativ längdändring, och är enhetslös. Spänning är kraft delad med stavens tvärsnittsarea, och har alltså samma enhet som tryck. Stål har en hög elasticitetsmodul (200 gigapascal), gummi har en låg elasticitetsmodul (mindre är 0,1 GPa).
I tre dimensioner är det lite annorlunda, eftersom stavar kan bli lite smalare när de dras ut. Så för vågutbredning i tre dimensioner är det bulkmodulen som gäller, som är definierad som förhållandet mellan tryck och relativ volymändring. Det är det omvända av kompressibilitet. Skolböcker kan säga att vatten är inkompressibel, och det är sant att vattnets kompressibilitet är försumbar i förhållande till luft. Men den är inte noll, så bulkmodulen är inte oändlig. För vatten är den 2,2 GPa, mycket mindre än för stål, men 22 000 gånger så stor än för luft.
För ideala gaser är den isoterma bulkmodulen lika med gasens tryck, eftersom produkt av tryck och volym är konstant vid konstant temperatur. Så under standardförhållanden är det 105 Pa (tusen hektopascal). Men för ljud måste man använda den adiabatiska bulkmodulen, eftersom svängningarna är så snabba att det inte finns någon energiutväxling med omgivningen. För kväve och syre är den 40 % högre än trycket.
Alla ideala gaser har lika många molekyler per volymenhet. En heliumatom är 7 gånger lättare än en kvävemolekyl, så ljudhastigheten är lite mindre än tre gånger så hög.
Jag försöker reda ut begreppet elasticity. Hewitt skriver ju att hur fort ljudet färdas har med materialets elasticity att göra. Jag förstår inte ordet... Jag har tidigare tänkt i densitet eftersom "skolläroböcker" ofta tar upp det, att ljud färdas snabbare i vatten än luft på grund av att densiteten är högre i vatten. Men det resonemanget funkar ju inte längre. T ex helium har ju lägre densitet än luft, men i helium färdas ju ljudet fortare än i luft. Är det för att helium är så lätt och därför har "många molekyler" som kan krocka/volymenhet?
Det är mycket möjligt att det finns en del skolböcker som säger att ljudhastigheten är högre i vatten pga densitet, men det är strunt. Jag har försökt förmedla till er att svängningshastigheter är högre ju starkare den återställande kraften är, och lägre ju större trögheten (massan) är. Det gäller för svängningar av massor på fjädrar, det gäller även för våghastigheter på strängar och i material. Våghastighet är omvänt proportionell mot roten ur densitet.
Det är den återställande kraften som är så mycket större i vatten än i luft. I en stav (is, stål) är det elasticitetsmodulen, som definieras som förhållandet mellan mekanisk spänning och töjning. Töjning är relativ längdändring, och är enhetslös. Spänning är kraft delad med stavens tvärsnittsarea, och har alltså samma enhet som tryck. Stål har en hög elasticitetsmodul (200 gigapascal), gummi har en låg elasticitetsmodul (mindre är 0,1 GPa).
I tre dimensioner är det lite annorlunda, eftersom stavar kan bli lite smalare när de dras ut. Så för vågutbredning i tre dimensioner är det bulkmodulen som gäller, som är definierad som förhållandet mellan tryck och relativ volymändring. Det är det omvända av kompressibilitet. Skolböcker kan säga att vatten är inkompressibel, och det är sant att vattnets kompressibilitet är försumbar i förhållande till luft. Men den är inte noll, så bulkmodulen är inte oändlig. För vatten är den 2,2 GPa, mycket mindre än för stål, men 22 000 gånger så stor än för luft.
För ideala gaser är den isoterma bulkmodulen lika med gasens tryck, eftersom produkt av tryck och volym är konstant vid konstant temperatur. Så under standardförhållanden är det 105 Pa (tusen hektopascal). Men för ljud måste man använda den adiabatiska bulkmodulen, eftersom svängningarna är så snabba att det inte finns någon energiutväxling med omgivningen. För kväve och syre är den 40 % högre än trycket.
Alla ideala gaser har lika många molekyler per volymenhet. En heliumatom är 7 gånger lättare än en kvävemolekyl, så ljudhastigheten är lite mindre än tre gånger så hög.
söndag 21 februari 2010
En klurig uppgift

Den datorgenererade bilden ovan visar ett rektangulärt block av plast eller dylikt. Eller så kan det vara ett akvarium. Dess bakre vägg är gul och röd, undersidan är svart och vit. Givet är att alla rutor i bilden är fyrkanta. De runda förmålen är halva sfärer. Uppgiften är att bestämma blockets brytningsindex.
Detta föregriper lite stråloptiken, men Snells lag är nog bekant för er alla. Var inte oroliga: detta blir ingen tentauppgift för er. Det kan ta tid att hitta en lösning. Men egentligen borde det här problemet inte vara för svårt - det är bara något annorlunda än vanliga skolproblem i optik.
torsdag 18 februari 2010
Uppgifter ur Benson
Jag visade Newtons ringar med specialmonterade linser. Men det går också bra att se interferensfransar mellan två vanliga glasskivor, när man använder monokromatisk ljus av till exempel en natriumlampa.
När skiktet inte är smal i förhållande till våglängd, beror fransarna inte endast på tjocklek, utan även på reflektionsvinkel till ögat. Vid mycket tunna skikt ser man fransar av konstant tjocklek. Vid jämna tjockare skikt ser man fransar av konstant tjocklek. Se skiss nedan:

Vi gick igenom problem 37.1 i Benson, se figur:

Det är ett standardproblem, som följs av tolv likadana.
Sedan tog vi problem 37:20, som är med rätta markerat som ett snäpp svårare:
Signals received by two microwave antennas that are 80 cm apart are fed to the same amplifier midway between the antennas. In order to receive a strong signal at a wavelength of 3 cm, the output from the upper antenna has to be delayed by 5 rad. In which direction is the source – assuming it is very far away.

"Exercises" i Benson kap. 37: 10, 13, 24, 31, 34, 37, 40, 62, 73.
"Exercises" i Benson kap. 38: 1, 2, 7, 17, 21, 50.
Ni får gärna hjälpa varandra i kommentarfälten nedan.
När skiktet inte är smal i förhållande till våglängd, beror fransarna inte endast på tjocklek, utan även på reflektionsvinkel till ögat. Vid mycket tunna skikt ser man fransar av konstant tjocklek. Vid jämna tjockare skikt ser man fransar av konstant tjocklek. Se skiss nedan:

Vi gick igenom problem 37.1 i Benson, se figur:

Det är ett standardproblem, som följs av tolv likadana.
Sedan tog vi problem 37:20, som är med rätta markerat som ett snäpp svårare:
Signals received by two microwave antennas that are 80 cm apart are fed to the same amplifier midway between the antennas. In order to receive a strong signal at a wavelength of 3 cm, the output from the upper antenna has to be delayed by 5 rad. In which direction is the source – assuming it is very far away.

"Exercises" i Benson kap. 37: 10, 13, 24, 31, 34, 37, 40, 62, 73.
"Exercises" i Benson kap. 38: 1, 2, 7, 17, 21, 50.
Ni får gärna hjälpa varandra i kommentarfälten nedan.
onsdag 17 februari 2010
Mer om Adobe Connect
Bra svensk användarhandledning finns här.
Jag tror att jag ska använda samma "rum" för de återstående föreläsningarna. Det är 1FY80320100215. Jag öppnar rummet imorgon igen, i god tid innan föreläsningen. Jag stänger efter att jag har lagt ut länken till video-upptagningen.
Angående imorgon, det börjer med en kort presentation av Näktergalen.
Jag tror att jag ska använda samma "rum" för de återstående föreläsningarna. Det är 1FY80320100215. Jag öppnar rummet imorgon igen, i god tid innan föreläsningen. Jag stänger efter att jag har lagt ut länken till video-upptagningen.
Angående imorgon, det börjer med en kort presentation av Näktergalen.
tisdag 16 februari 2010
Bilder utan lins
Idag experimenterade jag lite med att ta bilder av interferensmönster. Jag tog bort linsen från kameran, och använde direkt projektion på CCD-sensorn. Ljuskällan var en natriumlampa (ganska monokromatisk). Först en bild med Pascos ram med fyra dubbelspaltar på rad:

Ramen var nära framför kameran. Man ser interferensmönstrens centrala områden bredvid varandra.
De andra bilderna tog jag längre ifrån spalten, ungefär 15 cm. Här en montage med två exponeringar. Båda spaltparen har samma inbördes avstånd, men i den övre bilden är spalten två gånger så breda som i den nedre.

Och en liknande jämförelse för två enkelspaltar, den ena två gånger bredare än den andra:

Men man kan också se mönstret med blotta ögat. Det är bara att hålla en dubbelspalt nära framför pupillen, mot en avlägsen någorlunda monokromatisk källa. Det är en ganska vacker syn.

Ramen var nära framför kameran. Man ser interferensmönstrens centrala områden bredvid varandra.
De andra bilderna tog jag längre ifrån spalten, ungefär 15 cm. Här en montage med två exponeringar. Båda spaltparen har samma inbördes avstånd, men i den övre bilden är spalten två gånger så breda som i den nedre.

Och en liknande jämförelse för två enkelspaltar, den ena två gånger bredare än den andra:

Men man kan också se mönstret med blotta ögat. Det är bara att hålla en dubbelspalt nära framför pupillen, mot en avlägsen någorlunda monokromatisk källa. Det är en ganska vacker syn.
Allmän frågespalt
Det framkom ett önskemål om en allmän frågespalt på bloggen. Här är den: fråga på! Och vem som helst får ge svar förstås.
måndag 15 februari 2010
söndag 14 februari 2010
Hemlaborationer på distans
Att mäta laservåglängder med en linjal (obs: 6 sidor, bläddra vidare)
Det fanns intresse för att bygga skokartongspektrometern som jag hade framme. Jag har sammanställt en del instruktioner här, fast skokartongen finns inte riktigt med där. Min version var inspirerad av Project Starlab spektrometer (finns att köpa hos Sagitta).
Nästa träff i Växjö är 12 eller 13 mars (skriv gärna i kommentarfält nedan om ni vill komma på fredag eller på lördag). Laborationen kommer att handla om stråloptik. Jag vet inte exakt än vad jag ska välja, men prylarna borde finnas på många skolor. Och annars finns den här optiklådan av Alga Science. Om man väljer den, är hemlaborationens uppgift att göra några bra foton på optiska fenomen.
Det fanns intresse för att bygga skokartongspektrometern som jag hade framme. Jag har sammanställt en del instruktioner här, fast skokartongen finns inte riktigt med där. Min version var inspirerad av Project Starlab spektrometer (finns att köpa hos Sagitta).
Nästa träff i Växjö är 12 eller 13 mars (skriv gärna i kommentarfält nedan om ni vill komma på fredag eller på lördag). Laborationen kommer att handla om stråloptik. Jag vet inte exakt än vad jag ska välja, men prylarna borde finnas på många skolor. Och annars finns den här optiklådan av Alga Science. Om man väljer den, är hemlaborationens uppgift att göra några bra foton på optiska fenomen.
lördag 13 februari 2010
Ljudhastighet i vatten
Under helgens distansträff gjordes en hel del mätningar av ljudhastigheten i vatten som funktion av temperatur. Vi kunde se att hastigheten ökade med temperatur, men att den inte ändrades mer för höga temperaturer. Enligt Martin Chaplin här inträffar maximum vid 74 °C. Orsaken är att den adiabatiska bulkmodulen har ett maximum (och kompressibiliteten ett minimum) vid 64 °C (samma källa).
Vi diskuterade om det skulle finnas en anomali i ljudhastigheten kring 4, där vatten har ett maximum i densitet. Det verkar som att det beror på ljudets frekvens, men det experimentella läget är kanske inte helt klart (samma källa).
Vi använde fasändringen för fortskridande vågor. Det är möjligt att göra mycket noggranna mätningar om man ändrar vattentemperatur utan att ändra avståndet mellan sändare och mottagare. Man kunde börja med kokande vatten, låta det kyla ner, och bara titta på oscilloskopbilden med de två sinusvågor. Det skulle vara ett bra sätt att bestämma vid vilken temperatur maximum inträffar. Med samma metod kan man undersöka om det finns ett minimum för kallt vatten.
Jag glömde visa stående ultraljudvågor i vatten. Små luft bubblor samlas vid noder (eller vid antinoder, jag är inte säker). Men ljudtrycket är så högt att det har en synlig effekt på vattnets brytningsindex. Om man tittar genom den stående vågen, ser man att bakgrunden är "räfflad". Jag ska försöka ta en bild.
Vi diskuterade om det skulle finnas en anomali i ljudhastigheten kring 4, där vatten har ett maximum i densitet. Det verkar som att det beror på ljudets frekvens, men det experimentella läget är kanske inte helt klart (samma källa).
Vi använde fasändringen för fortskridande vågor. Det är möjligt att göra mycket noggranna mätningar om man ändrar vattentemperatur utan att ändra avståndet mellan sändare och mottagare. Man kunde börja med kokande vatten, låta det kyla ner, och bara titta på oscilloskopbilden med de två sinusvågor. Det skulle vara ett bra sätt att bestämma vid vilken temperatur maximum inträffar. Med samma metod kan man undersöka om det finns ett minimum för kallt vatten.
Jag glömde visa stående ultraljudvågor i vatten. Små luft bubblor samlas vid noder (eller vid antinoder, jag är inte säker). Men ljudtrycket är så högt att det har en synlig effekt på vattnets brytningsindex. Om man tittar genom den stående vågen, ser man att bakgrunden är "räfflad". Jag ska försöka ta en bild.
torsdag 11 februari 2010
Diffraktion och interferens
Den icke-inspelade föreläsningen handlade om hur vågor inte alltid går rakt fram. Det visades redan med Huyghens konstruktion, man kan visa det med en vågtank, och det finns simuleringar. En bra simulering är den här på PhET. Kör den! Titta på effekt av frekvens på våglängd. Se hur vågorna går lite vid sidan om vad som skulle vara spaltens skugga.
Ta bort spalten och använd två droppande kranar, gärna med lite högra frekvens. Observera interferensmönstret. Lägg till en detektor, dra "pennskrivaren" till högger, och flytta mätpunkten till olika ställen. Se att det inte finns någon vågrörelse på nodlinjerna, där båda jämstarka sändare är i motfas med varandra.
Gå nu tillbaka till en droppare, och lägg in en dubbelspalt. Flytt den lite närmare dropparen, och gör hålen lite smalare. Se att mönstret är som med två sändare. Det är som i Huyghens konstruktion: de båda spalten är nya sändare, som är i fas med varandra för att de kommer båda från samma källa.
Fortsätt med ljud (kolla "particles" och jämför med "greyscale") och med laserljus. Observera att avstånden och tiderna är mycket mindre än för en vågtank, men att mönstret är egentligen samma. Men för ljus går det inte att se svängningarna, inte ens med det snabbaste oscilloskopet. Man kan bara mäta intensiteter. Klicka därför på "show screen" och kanske också på "intensity graph".
Det var simuleringar. Jämför med en bild gjord med en kamera:

Spalten var 20 mikrometer bred, och var placerad på ett borrat hål i skyddslocket för en systemkamera (ingen lins). Den övre remsan visar bilden. De andra remsorna visar hur mönstret ser ut i de separata kanalerna för Röd, Grön och Blå. Längre vågor avlänkas mer, och det finns en tydlig effekt av våglångd för var minima hamnar. RGB-bilden ger de primära färgernas komplementärfärger: gul där blå har ett minimum, magenta där gröna våglängder utslocknar varandra, och cyan där rött ljus saknas.
Samma färger ser man också som fransar av konstant tjocklek i den här bilden av en såphinna på ett vinglas. Orsaken är interferens mellan ljus reflekterat från hinnans framsida och från hinnans baksida.
Ta bort spalten och använd två droppande kranar, gärna med lite högra frekvens. Observera interferensmönstret. Lägg till en detektor, dra "pennskrivaren" till högger, och flytta mätpunkten till olika ställen. Se att det inte finns någon vågrörelse på nodlinjerna, där båda jämstarka sändare är i motfas med varandra.
Gå nu tillbaka till en droppare, och lägg in en dubbelspalt. Flytt den lite närmare dropparen, och gör hålen lite smalare. Se att mönstret är som med två sändare. Det är som i Huyghens konstruktion: de båda spalten är nya sändare, som är i fas med varandra för att de kommer båda från samma källa.
Fortsätt med ljud (kolla "particles" och jämför med "greyscale") och med laserljus. Observera att avstånden och tiderna är mycket mindre än för en vågtank, men att mönstret är egentligen samma. Men för ljus går det inte att se svängningarna, inte ens med det snabbaste oscilloskopet. Man kan bara mäta intensiteter. Klicka därför på "show screen" och kanske också på "intensity graph".
Det var simuleringar. Jämför med en bild gjord med en kamera:

Spalten var 20 mikrometer bred, och var placerad på ett borrat hål i skyddslocket för en systemkamera (ingen lins). Den övre remsan visar bilden. De andra remsorna visar hur mönstret ser ut i de separata kanalerna för Röd, Grön och Blå. Längre vågor avlänkas mer, och det finns en tydlig effekt av våglångd för var minima hamnar. RGB-bilden ger de primära färgernas komplementärfärger: gul där blå har ett minimum, magenta där gröna våglängder utslocknar varandra, och cyan där rött ljus saknas.
Samma färger ser man också som fransar av konstant tjocklek i den här bilden av en såphinna på ett vinglas. Orsaken är interferens mellan ljus reflekterat från hinnans framsida och från hinnans baksida.
onsdag 10 februari 2010
Föreläsningen går live
Nu verkar all ny hårdvara på plats och alla nya program och drivers vara installerade. Imorgon hoppar jag i djupet. Jag ska försöka sända föreläsningen live via Adobe Connect. En kamera ska filma mig, och dessutom ska projektorns skärm sändas. Om jag använder Smartboard, kommer man att se hur anteckningarna där växer fram.
Adressen är https://connect.sunet.se/r75275183/
Sändningen börjar klockan 13:00, och ska streamas live i två timmar.
Man kan chatta och ge feedback på detta sätt, men jag kommer nog inte att följa vad som skrivs där. Chatta med varandra.
Föreläsningen ligger kvar, så man kan också titta på den senare.
Adobe Connect rekommenderar att man installerar en plugin. För mig gick det snabbt att installera det.
Men detta blir ett test. Jag kör också backup på vanligt sätt.
PS: Webcastning var live, men ingen upptagning har gjorts. Och dessutom glömde jag sätta backup igång :(
Adressen är https://connect.sunet.se/r75275183/
Sändningen börjar klockan 13:00, och ska streamas live i två timmar.
Man kan chatta och ge feedback på detta sätt, men jag kommer nog inte att följa vad som skrivs där. Chatta med varandra.
Föreläsningen ligger kvar, så man kan också titta på den senare.
Adobe Connect rekommenderar att man installerar en plugin. För mig gick det snabbt att installera det.
Men detta blir ett test. Jag kör också backup på vanligt sätt.
PS: Webcastning var live, men ingen upptagning har gjorts. Och dessutom glömde jag sätta backup igång :(
tisdag 9 februari 2010
Elektromagnetiska vågor
Historisk utveckling:
Hastigheten för dessa vågor som var lösningar till Maxwells ekvationer sammanföll alltså med ljusets hastighet. Maxwell var den första som förstod vad ljus var.
Ljusets hastighet är alltså given av naturlagar. Hewitts resonemang i kapitel 26 utifrån energins bevarande visar väl varför hastigheten inte kan vara större eller mindre i ett medium. Men hans resonemang övertyger inte om det märkliga med ljusets hastighet i vakuum, att denna hastighet är absolut och densamma för olika observatörer som rör sig i förhållande till varandra. Det går emot vår intuition. Det var Einstein som insåg att tid är relativ, och att "samtidig" inte är något väldefinierat begrepp när olika iakttagare är i rörelse relativt till varandra.
Det är inte helt uppenbart hur man ska tolka bilder som den här. Figuren ser nästan ut som en transversell våg på ett snöre, och matematiken är nästan densamma, men likheterna kan vara lite bedrägliga. För elektriska vågor har sinuskurvan ingen motsvarig form i verkligheten. Sinuskurvan visar bara hur vektorfältens riktningar varierar i rummet, längs en linje.
Det är viktigt att veta att vektorfältet fyller hela rummet. Jag försökte rita det på tavlan, i tvådimensioner och vid en punkt i tid. Här kommer en animering:


- 1820 - HC Ørsted upptäcker att elektrisk ström påverkar kompassnål
- 1831 - Faraday upptäcker magnetisk induktion
- 1864 - JC Maxwell räknar ut att c=1/√(ɛμ) och han får 3,1.108 m/s.
Hastigheten för dessa vågor som var lösningar till Maxwells ekvationer sammanföll alltså med ljusets hastighet. Maxwell var den första som förstod vad ljus var.
Ljusets hastighet är alltså given av naturlagar. Hewitts resonemang i kapitel 26 utifrån energins bevarande visar väl varför hastigheten inte kan vara större eller mindre i ett medium. Men hans resonemang övertyger inte om det märkliga med ljusets hastighet i vakuum, att denna hastighet är absolut och densamma för olika observatörer som rör sig i förhållande till varandra. Det går emot vår intuition. Det var Einstein som insåg att tid är relativ, och att "samtidig" inte är något väldefinierat begrepp när olika iakttagare är i rörelse relativt till varandra.
Det är inte helt uppenbart hur man ska tolka bilder som den här. Figuren ser nästan ut som en transversell våg på ett snöre, och matematiken är nästan densamma, men likheterna kan vara lite bedrägliga. För elektriska vågor har sinuskurvan ingen motsvarig form i verkligheten. Sinuskurvan visar bara hur vektorfältens riktningar varierar i rummet, längs en linje.
Det är viktigt att veta att vektorfältet fyller hela rummet. Jag försökte rita det på tavlan, i tvådimensioner och vid en punkt i tid. Här kommer en animering:


torsdag 4 februari 2010
Delfiner
I kapitel 20 säger Hewitt saker om delfiner som är något förvånande. Visst, de använder någon typ av sonar för att lokalisera fiskstim. Visst simblåsor och lungor reflekterar ljud mycket bra (reflektion av öppen ände), och även ben (reflektion av tätare material).

Men jag undrar om delfiner kan se tumörer och hjärtattacker – Hewitt ger ingen referens. Och när han skriver att de kan se ens "emotionella tillstånd", misstänker jag att allt detta bottnar i New Age svärmerier.

Men jag undrar om delfiner kan se tumörer och hjärtattacker – Hewitt ger ingen referens. Och när han skriver att de kan se ens "emotionella tillstånd", misstänker jag att allt detta bottnar i New Age svärmerier.
tisdag 2 februari 2010
Sonogram och resonanser
Programmet som jag försökte visa igår är iSpectrum. Programmet finns bara för Macintosh, men liknande gratisprogram finns för Windows. Här ett spektrogram av en flicka som säger "Oh no!"


lördag 30 januari 2010
Toner och övertoner
Kapitel 21 i Hewitt handlar om sådana ljud som har en tonhöjd. Dessa ljud orsakas av periodiska svängningar, men det är sällan att det är enkla sinusvågor. Ljudets svängningarna är för snabba för att kunna följa med blotta ögat. Därför behövs det oscilloskop, ett slags "tidmikroskop" för att kunna se vad som händer i små tidsintervaller. Vi har förstås oscilloskop i kurslabbet, men för ljud kan ni också använda era egna datorer, särskilt om den har en inbyggd mikrofon. Ett program som är mycket bra för detta är MacScope II (som faktiskt också finns för Windows). Jag föreslår att ni som brukar ta med era bärbara, att ni installerar programmet. Då kan vi titta på olika ljud under de praktiska övningarna.
(Videosnutten ovan finns i bättre upplösning här.)
(Videosnutten ovan finns i bättre upplösning här.)
fredag 29 januari 2010
Om ljud, oljud och luft
Här lite föreläsningsanteckningar. Det är ungefär vad jag skrev på tavlan igår. (Det var något fel med videofilmen igår, men det är fixat nu).
torsdag 28 januari 2010
Luft och lukt
Föreläsningen idag handlade mycket om luft som medium för ljud. Jag ska skriva om det senare. Men först lite om Exercise 18 av kapitel 19 i Hewitt, som handlar om att öppna en gaskran.
Om det sker på några meters avstånd, hör man gasets sus nästan omedelbart, men det dröjer innan man kan lukta det. Hewitts fråga är vad det säger oss om ljudhastigheten och molekylrörelserna i mediet som bär ljudvågorna.
Vad tycker ni att svaret är?
Om det sker på några meters avstånd, hör man gasets sus nästan omedelbart, men det dröjer innan man kan lukta det. Hewitts fråga är vad det säger oss om ljudhastigheten och molekylrörelserna i mediet som bär ljudvågorna.
Vad tycker ni att svaret är?
måndag 25 januari 2010
Hemlab - slinky
Idag genomförde campusstudenterna en laboration med slinkys. Distansstudenterna har det svårare: ni måste själva få tag i en slinky, och ni behöver kanske be någon att hjälpa till. Det behövs ingen avancerad utrustning: om man skulle sakna måttband, kan man ta steg; stoppur finns på nätet; slinkyns massa kan man bestämma med en improviserad balans.
Det svåraste är att bestämma spännkraften i slinkyn. På campus använde vi fjäderdynamometrar med skala i newton. Hemma kan man spänna slinkyn så långt att den matchar en känd kraft, till exempel tyngdkraften från en grej med en massa på 100 eller 200 gram (sådant kan finnas i köket). Sedan får man improvisera någon trissa för att få spännkraften horisontell. Om man så har bestämt en lämplig längd med en lämplig kraft, kan man sätta igång.
Uppgiften är att bestämma utbredningshastighet för transversella vågor med två olika experiment. Det ena sättet är med fortskridande vågor, det andra med stående vågor. Dessa värden ska man jämföra med ett teoretiskt värde utifrån slinkyns spänning och dess tröghet.
Det som var så bra med laborationen på campus var samarbetet. Det kan vi också göra här. Skriv era idéer och era resultat i kommentarer nedan. Och ja, detta är obligatoriskt...
Det svåraste är att bestämma spännkraften i slinkyn. På campus använde vi fjäderdynamometrar med skala i newton. Hemma kan man spänna slinkyn så långt att den matchar en känd kraft, till exempel tyngdkraften från en grej med en massa på 100 eller 200 gram (sådant kan finnas i köket). Sedan får man improvisera någon trissa för att få spännkraften horisontell. Om man så har bestämt en lämplig längd med en lämplig kraft, kan man sätta igång.
Uppgiften är att bestämma utbredningshastighet för transversella vågor med två olika experiment. Det ena sättet är med fortskridande vågor, det andra med stående vågor. Dessa värden ska man jämföra med ett teoretiskt värde utifrån slinkyns spänning och dess tröghet.
Det som var så bra med laborationen på campus var samarbetet. Det kan vi också göra här. Skriv era idéer och era resultat i kommentarer nedan. Och ja, detta är obligatoriskt...
Doppler och Tjerenkov
Det finns en underbar videosnutt på physicsplace.com med hur Hewitt förklarar doppler-effekt med en simmande insekt. Det finns inte så mycket för mig att lägga till. På sajten har Hewitt också en bra interaktiv simulering, där det även finns bra kvantitativa testfrågor. Gör dessa!
Christian Doppler beskrev en teori om färgen av dubbelstjärnor 1842. Tre år senare skrev Buys Ballot om hur man kunde höra det som en tonhöjdsskillnad i ljud. Men egentligen var det redan Ole Rømer som använde den halvårsvisa periodförskjutningen av Jupiters månar för att bestämma ljusets hastighet.

Animationen ovan visar vad som händer när insekten simmer snabbare än våghastigheten. (Klicka på den om den inte sätter igång.) Det uppstår ett "V", en bogvåg, en typ av chockvåg. Om något rör sig genom luft i överljudsfart, har chockvågen formen av en kon. När dess kägelsnitt på jordytan (en hyperbel) passerar någon, hör denne en ljudbang (sonic boom).
Något liknande kan hända när partiklar färdas snabbare än ljuset. Visst. det kan hända ... i material. I vatten är ljudhastigheten bara 75 % av ljusets hastighet i vakuum. Neutroner från kärnreaktioner rör sig snabbare än så. När de knuffar mot väte-kärnor i vatten, får man en laddad partikel i överjusfart. Det ger upphov till Tjerenkovstrålning, det blå ljuset i en reaktorbassäng.
Sådana ljusblixtar i vatten kan orsakas av partiklar som uppstår genom reaktioner med neutriner. Man kan använda klara sjöar eller sydpolens is som detektorer för neutrinoastromi (fysiker från Linné universitet har varit inblandade). Även i atmosfären är ljusets hastighet lägre än i vakuum. Så kan Tjerenkovstrålning högt i luften användas för att detektera kosmisk strålning med extremt höga energier.
Christian Doppler beskrev en teori om färgen av dubbelstjärnor 1842. Tre år senare skrev Buys Ballot om hur man kunde höra det som en tonhöjdsskillnad i ljud. Men egentligen var det redan Ole Rømer som använde den halvårsvisa periodförskjutningen av Jupiters månar för att bestämma ljusets hastighet.

Animationen ovan visar vad som händer när insekten simmer snabbare än våghastigheten. (Klicka på den om den inte sätter igång.) Det uppstår ett "V", en bogvåg, en typ av chockvåg. Om något rör sig genom luft i överljudsfart, har chockvågen formen av en kon. När dess kägelsnitt på jordytan (en hyperbel) passerar någon, hör denne en ljudbang (sonic boom).
Något liknande kan hända när partiklar färdas snabbare än ljuset. Visst. det kan hända ... i material. I vatten är ljudhastigheten bara 75 % av ljusets hastighet i vakuum. Neutroner från kärnreaktioner rör sig snabbare än så. När de knuffar mot väte-kärnor i vatten, får man en laddad partikel i överjusfart. Det ger upphov till Tjerenkovstrålning, det blå ljuset i en reaktorbassäng.
Sådana ljusblixtar i vatten kan orsakas av partiklar som uppstår genom reaktioner med neutriner. Man kan använda klara sjöar eller sydpolens is som detektorer för neutrinoastromi (fysiker från Linné universitet har varit inblandade). Även i atmosfären är ljusets hastighet lägre än i vakuum. Så kan Tjerenkovstrålning högt i luften användas för att detektera kosmisk strålning med extremt höga energier.
Peer-instruction
Först lite om video-länkarna. Det beror lite på ens browser och inställningar vad som händer när man klickar på länkarna. Man behöver inte ladda ner dessa stora filer för att se dem. Man kan kopiera url till QuickTime, så börjar filmen spela med en gång. Då är det också lätt att flytta fram till föreläsningens andra timme, till exempel.
Sedan lite om klassen på physicsplace.com. Om man har 11e utgåvan, kommer man inte in med Class ID som jag gav på första lektionen. För er har jag nu skapat en ny klass med Class ID cm219115.
Föreläsningens första timme ägnade vi oss åt Peer Instruction. På ett lite low-tech sätt - utan fjärrkontroller. Och nästa gång jag kanske använder färjade bokstavskort. Men det blev också en del bra diskussion så här. För frågorna se .pdf-fil. Det är ett urval ur en större bunt clicker-frågor gjorda av Trish Loeblein.
Sedan lite om klassen på physicsplace.com. Om man har 11e utgåvan, kommer man inte in med Class ID som jag gav på första lektionen. För er har jag nu skapat en ny klass med Class ID cm219115.
Föreläsningens första timme ägnade vi oss åt Peer Instruction. På ett lite low-tech sätt - utan fjärrkontroller. Och nästa gång jag kanske använder färjade bokstavskort. Men det blev också en del bra diskussion så här. För frågorna se .pdf-fil. Det är ett urval ur en större bunt clicker-frågor gjorda av Trish Loeblein.
fredag 22 januari 2010
Reflektion och stående vågor

I torsdags blev jag själv lite osäker om tecken vid reflektion av vågor på en sträng. Så jag räknade ut några animationer med programmet Mathematica. Därför har jag också laddat upp en animation med en enkelpuls, se ovan. Pricken är den blå strängens ände. Det röda är en "speglad" våg. När dess utvikelse vid änden är av motsatt tecken, är det samma som när änden sitter fast i en vägg. Denna animation visar tydligare och mer pedagogiskt att en puls vid reflektion av fast ände kommer tillbaka med negativt tecken.
Men det är ändå instruktivt med en dubbelpuls. Det visar hur en stående våg kan uppstå vid reflektion av fast ände.

Efter en halv period ser man att den reflekterade vågen är i fas med den infallande vågen. Om samma effekt uppstår vid strängens andra ände, och om strängens längd är en halv våglångd, uppstår en stående våg.
Matematiskt kan en enkelt harmonisk stående våg skrivas som en summa av två fortskridande vågor: en sinusvåg som går till höger och en likadan sinusvåg som går till vänster.
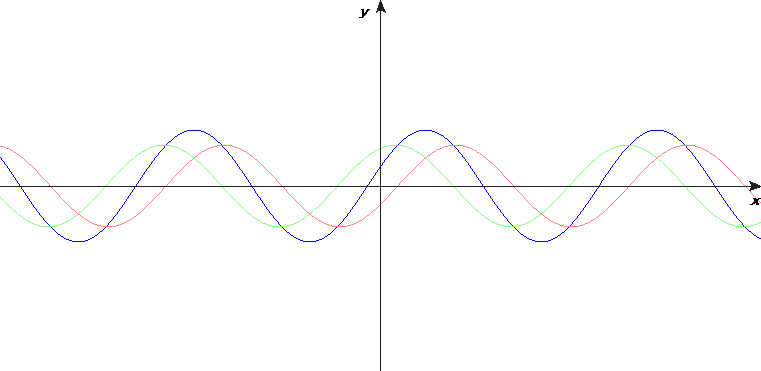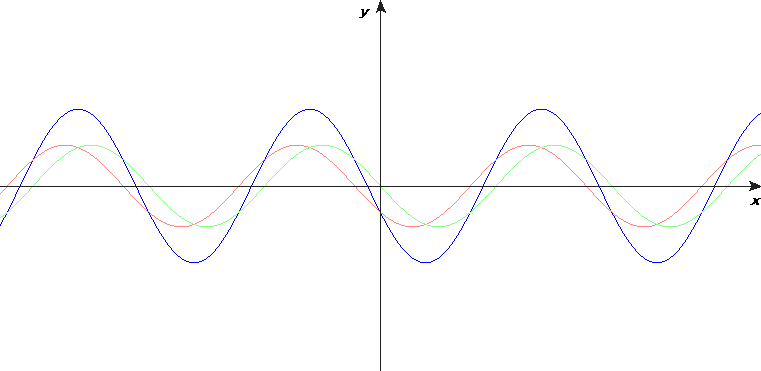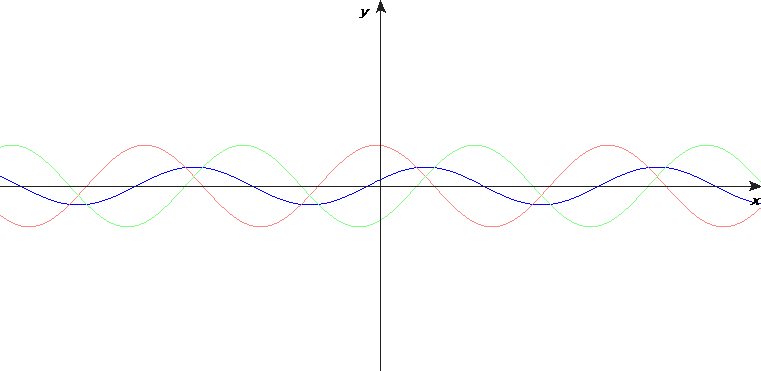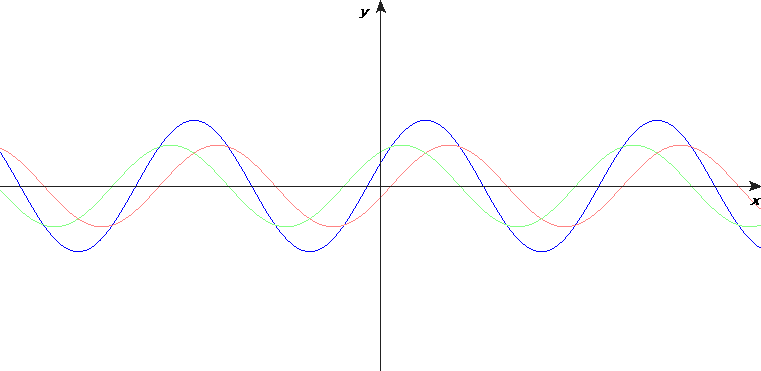
Om resonans uppstår, är förhållandet mellan våglängden och avståndet mellan änderna så att fasta änder ligger vid en nod och fria änder vid en buk.
torsdag 21 januari 2010
Vågutbredning
Jag kopplade ihop två vagnar med fjädrar på mekanik-banan. Om jag nu ger den ena vagnen en knuff, börjar också den andra röra sig. Om jag hade många vagnar och fler fjädrar, skulle man kunna se att en puls utbreder sig längs med banam. Det går att följa med ögat, eftersom vagnarna har stor massa och fjädrarnas kraftkonstant är liten.
Men i princip sker samma sak i Newtons vagga. Eller när man slår med en hammare på en järnstav. Det är bara att massan är mycket med finfördelad och att kraftkonstanterna mellan atomerna är mycket större i förhållande till deras massor. Det ger en hög utbredningshastighet: typ 5 km/sekund i stål. Men principen är densamma.
Denna lektion handlar mest om transversella vågor på strängar. Mest för att det är lätt att rita vad som händer. Det finns en mycket bra simulering på sajten PhET. Om man vill se sådana vågor på riktigt, går det bra med en Slinky eller med till exempel ett hopprep.
Men i princip sker samma sak i Newtons vagga. Eller när man slår med en hammare på en järnstav. Det är bara att massan är mycket med finfördelad och att kraftkonstanterna mellan atomerna är mycket större i förhållande till deras massor. Det ger en hög utbredningshastighet: typ 5 km/sekund i stål. Men principen är densamma.
Denna lektion handlar mest om transversella vågor på strängar. Mest för att det är lätt att rita vad som händer. Det finns en mycket bra simulering på sajten PhET. Om man vill se sådana vågor på riktigt, går det bra med en Slinky eller med till exempel ett hopprep.
måndag 18 januari 2010
Good vibrations
Kursen handlar om vågor. Liknande fysikaliska fenomen förekommer vid många typer av vågor, och vågor kan beskrivas med samma slags matematiska modeller. Ett exempel är "vågen" på stadionsläktare.
Det är inte så mycket fysikaliska växelverkninger i det, men "vågen" visar en viktig sak mycket tydlig: vågen utbreder sig, men det är inte människorna som springer runt. De stannar på sin sittplats, bara står upp och sätter sig. Det är samma sak med vattenvågor och med vågor på en slinky (en leksak som ni bör köpa om ni inte redan har).
Vågor är rörelser i tid och rum, men vi tittar först på enkla svängningar, periodiska funktioner av bara en variabel: tid. Jag visade en vagn på en bana mellan fjädrar, filmsnutten ser man här:
Man ser att fjädrarna drar vagnen tillbaka till jämviktsläget. Men den stannar inte där, på grund av dess tröghet: i jämviktsläget verkar ingen kraft, och enligt Newtons första lag fortsätter massan med samma hastighet. Dock då verkar fjäderkraften åt andra hållet. Vagnen bromsas upp tills hastigheten är noll i vändpunkten, där den återställande kraften är störst. Den blå lådan på vagnen är en accelerometer. Den visar tydligt att vagnens acceleration är proportionell mot fjädrarnas återställande kraft, och att den är proportionell mot utvikelsen, men av motsatt tecken.
Med Pasco-programmet DataStudio kan vi göra en registrering av utvikelsen som funktion av tid:
(Blogspot har komprimerat, jag ska också lägga ut skärminspelningen i original.)
Jag lägger ut mina föreläsningsanteckningar:
Det är inte så mycket fysikaliska växelverkninger i det, men "vågen" visar en viktig sak mycket tydlig: vågen utbreder sig, men det är inte människorna som springer runt. De stannar på sin sittplats, bara står upp och sätter sig. Det är samma sak med vattenvågor och med vågor på en slinky (en leksak som ni bör köpa om ni inte redan har).
Vågor är rörelser i tid och rum, men vi tittar först på enkla svängningar, periodiska funktioner av bara en variabel: tid. Jag visade en vagn på en bana mellan fjädrar, filmsnutten ser man här:
Man ser att fjädrarna drar vagnen tillbaka till jämviktsläget. Men den stannar inte där, på grund av dess tröghet: i jämviktsläget verkar ingen kraft, och enligt Newtons första lag fortsätter massan med samma hastighet. Dock då verkar fjäderkraften åt andra hållet. Vagnen bromsas upp tills hastigheten är noll i vändpunkten, där den återställande kraften är störst. Den blå lådan på vagnen är en accelerometer. Den visar tydligt att vagnens acceleration är proportionell mot fjädrarnas återställande kraft, och att den är proportionell mot utvikelsen, men av motsatt tecken.
Med Pasco-programmet DataStudio kan vi göra en registrering av utvikelsen som funktion av tid:
(Blogspot har komprimerat, jag ska också lägga ut skärminspelningen i original.)
Jag lägger ut mina föreläsningsanteckningar:
Introduktionsmöte
Så träffades vi på kursens introduktionsmöte, i alla fall campusstudenterna i Växjö. Det ser ut som ett bra gäng! Vi bestämde laborationer på onsdag eftermiddagar - jag har lagt in två datum i schemat på studentportalen.
Jag visade kursböckerna. Hewitts Conceptual Physics är grunden för kursen. Den ger på ett mycket trevligt sätt bra förklaringar och en god förståelse för fysiken i kursen. I priset ingår tillgång till en bra webbsajt, där man kan kolla att man har förstått (skrapkod finns i boken). Class ID är cm914674 (men jag kommer inte att använda era svar där för att sätta betyg).
Men vi vill nå lite längre, och också använda den matematiken som vi kan. Det görs i många fysikböcker. Till exempel i Bensons University Physics, men vilken som helst "calculus based" usonsk fysikbibel duger bra. (Om man köper en bok utgiven hos Pearson, får man tillgång till sajten masteringphysics.com.) Man kan också ta en bok som handlar mer specifikt om vägörelseläre, till exempel "Dynamic fields and waves" av Open University i England (framtagen för distansundervisning). Mindre färgglatt men på svenska är Våglära och optik av Göran Jönsson.
Jag visade kursböckerna. Hewitts Conceptual Physics är grunden för kursen. Den ger på ett mycket trevligt sätt bra förklaringar och en god förståelse för fysiken i kursen. I priset ingår tillgång till en bra webbsajt, där man kan kolla att man har förstått (skrapkod finns i boken). Class ID är cm914674 (men jag kommer inte att använda era svar där för att sätta betyg).
Men vi vill nå lite längre, och också använda den matematiken som vi kan. Det görs i många fysikböcker. Till exempel i Bensons University Physics, men vilken som helst "calculus based" usonsk fysikbibel duger bra. (Om man köper en bok utgiven hos Pearson, får man tillgång till sajten masteringphysics.com.) Man kan också ta en bok som handlar mer specifikt om vägörelseläre, till exempel "Dynamic fields and waves" av Open University i England (framtagen för distansundervisning). Mindre färgglatt men på svenska är Våglära och optik av Göran Jönsson.
Prenumerera på:
Kommentarer (Atom)



