Reflektion och stående vågor

I torsdags blev jag själv lite osäker om tecken vid reflektion av vågor på en sträng. Så jag räknade ut några animationer med programmet Mathematica. Därför har jag också laddat upp en animation med en enkelpuls, se ovan. Pricken är den blå strängens ände. Det röda är en "speglad" våg. När dess utvikelse vid änden är av motsatt tecken, är det samma som när änden sitter fast i en vägg. Denna animation visar tydligare och mer pedagogiskt att en puls vid reflektion av fast ände kommer tillbaka med negativt tecken.

Men det är ändå instruktivt med en dubbelpuls. Det visar hur en stående våg kan uppstå vid reflektion av fast ände.


Efter en halv period ser man att den reflekterade vågen är i fas med den infallande vågen. Om samma effekt uppstår vid strängens andra ände, och om strängens längd är en halv våglångd, uppstår en stående våg.

Matematiskt kan en enkelt harmonisk stående våg skrivas som en summa av två fortskridande vågor: en sinusvåg som går till höger och en likadan sinusvåg som går till vänster.



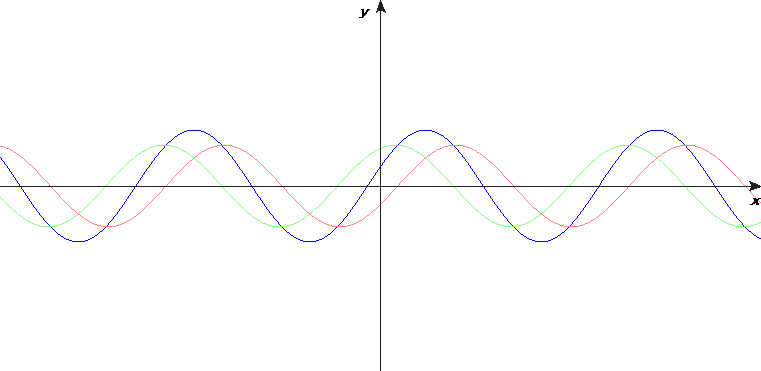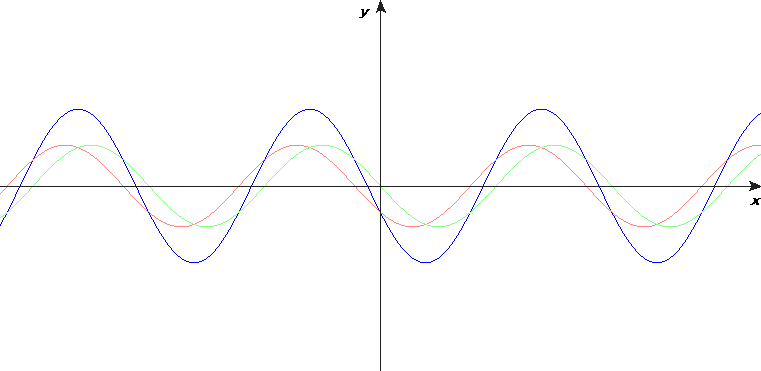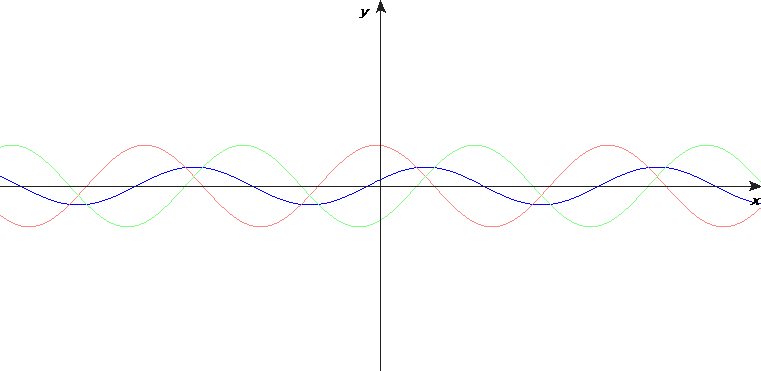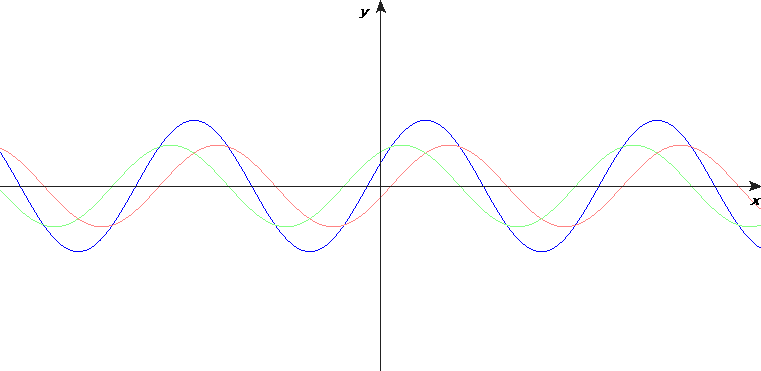
Om resonans uppstår, är förhållandet mellan våglängden och avståndet mellan änderna så att fasta änder ligger vid en nod och fria änder vid en buk.